Нашел на компьютере потерянную статью. Довольно давно собирался опубликовать ее в ЖЖ. В итоге публикую в своем новом блоге.
Итак, сначала задача. Есть аудитория интернета, состоящая из N пользователей (N — известное большое число). И есть некий сайт, количество посетителей которого A требуется узнать. Спрашивать у всех N пользователей, посещали ли они нужный сайт, накладно, а в некоторых случаях и чревато. Поэтому опрашивается небольшая выборка из n пользователей, при том что n обычно значительно меньше N. По тому, сколько людей из выборки посетили наш сайт, делаются выводы о том, сколько посетителей сайта среди всей интернет-аудитории.
В качестве примера возьму прекрасно известный в рунете сайт, а именно «Афишу». Тем более я работал с оптимизацией их сервиса.
Теперь собственно матчасть (тем, кто не знаком с основами теории вероятностей, будет тяжело).
Рассмотрим следующую случайную величину:
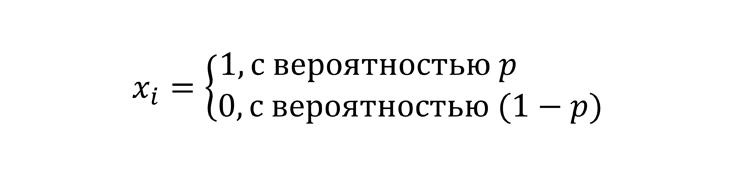
Где p=A/N — вероятность того, что отдельный взятый пользователь из рассматриваемой аудитории интернета посетил наш сайт (напоминаю, что A — неизвестное искомое значение, то есть p нам тоже неизвестно). Эта случайная величина принимает значение 1, если i-й интернет-пользователь оказался посетителем нужного сайта, и значение 0 в противном случае.
Что можно сказать про эту случайную величину? Мы можем посчитать ее математическое ожидание и дисперсию:
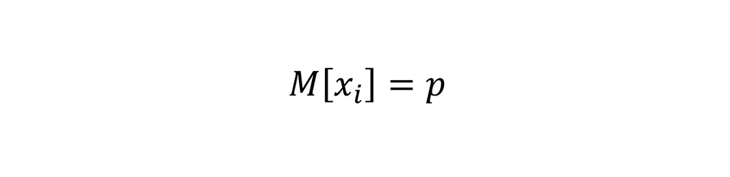
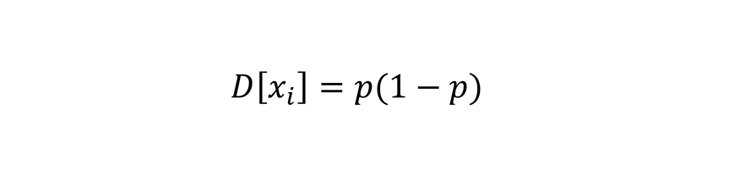
Важно, что вероятность p — это не случайная величина, а вполне определенная, хоть и неизвестная величина.
Из всей рассматриваемой аудитории интернета отберем n пользователей — это будет наша выборка (n — известное число).
Рассмотрим теперь другую случайную величину:
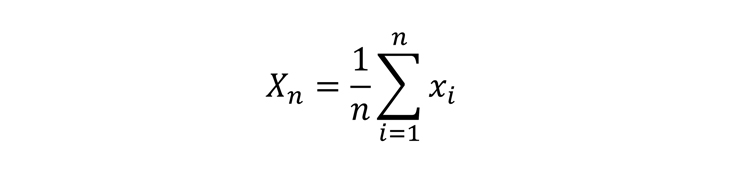
Эта случайная величина отражает долю посетителей сайта среди пользователей, отобранных в нашу выборку. Случайная — значит, может принимать любые значения от 0 до 1 в зависимости от того, как мы будем отбирать пользователей в выборку. Для этой случайной величины мы можем посчитать, а точнее вывести формулу математического ожидания и дисперсии:
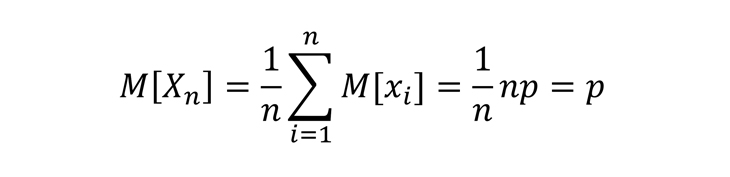
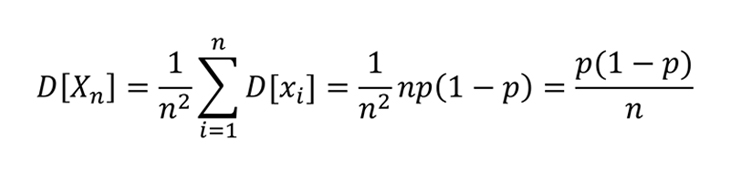
Получается, что сформированная нами случайная величина Хn имеет математическое ожидание, равное искомому параметру p, который фактически определяет долю аудитории интернета, которая посетила наш сайт. А дисперсия этой случайной величины уменьшается при увеличении размера выборки. То есть можно взять достаточно большую выборку и принять реализацию случайной величины Хn за оценку доли посетителей сайта среди всех пользователей, а затем и получить искомое A — количество таких посетителей.
Главный же фокус заключается в том, что при достаточно больших n можно считать, что случайная величина Хn имеет нормальное (a.k.a. гауссовское) распределение. А для нормального распределения известна функция распределения, с помощью которой легко можно рассчитывать квантили, то есть определять, с какой вероятностью значения этой случайной величины будут лежать в заданном интервале (или, наоборот, в каком интервале будут лежать значения случайной величины при заданной доверительной вероятности).
Чтобы двигаться дальше, понадобится избавиться от дисперсии и перейти к сигме.
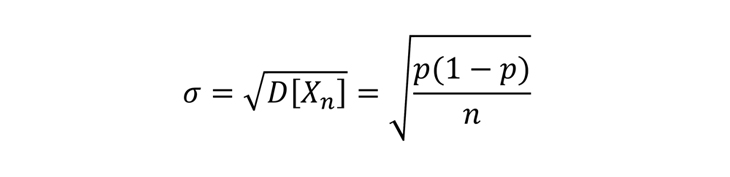
Сигма определяет отклонение случайной величины от своего математического ожидания (среднего) и понадобится нам дальше при построении доверительных интервалов.
Итак, поскольку Хn имеет нормальное распределение, имеет место следующее равенство:
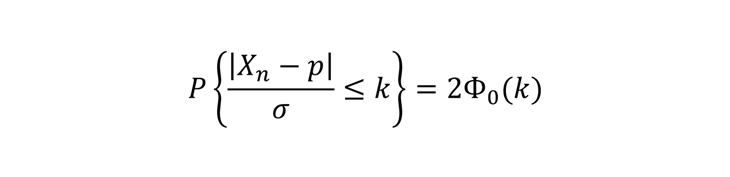
Здесь P — это обозначение вероятности, Ф0 — функция Лапласа, значение которой при заданном аргументе k можно получить из таблицы (или, наоборот, при заданном значении функции Лапласа можно получить ее аргумент). А все вместе это означает, что вероятность того, что случайная величина Хn отклонится от своего мат.ожидания не больше чем на k сигм, равна удвоенной функции Лапласа от k.
На примере этот ад становится гораздо понятнее.
Пример 1.
Возьмем российскую интернет-аудиторию. Согласно TNS за месяц в интернет выходят около 27 миллионов человек (ну, в рамках заданных TNS ограничений). Значит, N = 27 миллионов. Выборка у TNS cоставляет около 10 тысяч. Ок, n = 10 тысяч. Сайт, который мы рассматриваем – Afisha.ru, конечно. Согласно TNS, месячная российская аудитория в июле была равна около 2,7 миллионов человек, то есть A = 2,7 млн, а p = A/N = 0,1. Подставляем эти данные в формулу сигмы, получаем, что сигма = 0,003. Допустим, мы хотим понять, в каком интервале лежит реальное значение российского охвата Афиши при уровне доверительной вероятности в 90%.
2Ф0(k)=0,9
Ф0(k)=0,45
k = 1,645 (получается из таблицы значение функции Лапласа)
С вероятностью 90% реальная доля посетителей Афиши среди всей аудитории интернета равна p±kσ = 0,1±0,005, то есть лежит где-то между 0,095 и 0,105. Или в абсолютных значениях с вероятностью 90% реальный российский охват Афиши равен 2,7 млн ± 0,133 млн, то есть лежит где-то между 2,567 млн и 2,833 млн.
Если повысить уровень доверительной вероятности до 99%, то:
2Ф0(k)=0,99
Ф0(k)=0,495
k = 2,58
С вероятностью 99% реальная доля посетителей Афиши среди всей аудитории интернета равна 0,1±0,008, то есть лежит где-то между 0,092 и 0,108. Или в абсолютных значениях с вероятностью 99% реальный российский охват Афиши равен 2,7 млн ± 0,209 млн, то есть лежит где-то между 2,491 млн и 2,909 млн.
На этом месте стоит сделать несколько полезных наблюдений:
1. Из формулы сигмы видно, что отклонение тем меньше, чем больше размер выборки. И наоборот, чем меньше выборка, тем больше отклонение.
2. Из той же формулы видно, что отклонение тем меньше, чем меньше размер оцениваемого параметра p (доли аудитории нашего сайта во всей интернет-аудитории). Однако если посчитать относительное отклонение, то есть отклонение в сравнении с математическим ожиданием, то получим:
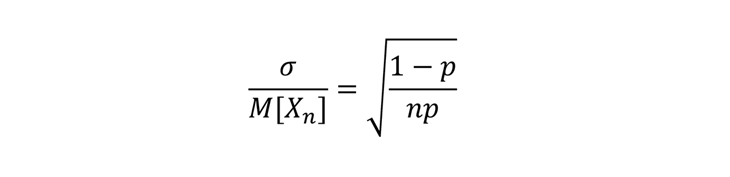
Видно, что при уменьшении p (чем ближе p к нулю) относительное отклонение увеличивается. Это хорошо видно на примере.
Пример 2.
Берем ту же российскую аудиторию. Но теперь посчитаем сайт поменьше — с охватом 270 тысяч посетителей в месяц. Размер выборки оставляем тот же — 10 тысяч.
p = M/N = 0,01
σ = 0,001
Таким образом, с 90% вероятностью реальная доля аудитории сайта среди всей аудитории интернета будет 0,01±0,0016. То есть относительное отклонение будет равно ±0,0016/0,01*100% = ±16%. Тогда как для примера 1 относительное отклонение при 90% уровне доверительной вероятности было равно ±5%.
Если взять сайт еще меньше — с месячным охватом в 27 тысяч посетителей. То относительное отклонение при том же уровне доверительной вероятности и размере выборки получится ±52%, что уже вряд ли можно назвать точной оценкой.
Само собой, описанная выше теория работает только тогда, когда выборка является репрезентативной, то есть по своей структуре повторяет структуру всей интернет-аудитории. Почему репрезентативность важна?
В самом начале была рассмотрена случайная величина xi, отражающая, является ли отдельно взятый интернет-пользователь посетителем нашего сайта. Вероятность p, фигурирующая в определении этой случайной величины посчитана в среднем для всей интернет-аудитории. При этом понятно, что на самом деле эта вероятность сильно отличается у разных групп интернет-пользователей — у московской молодежи вероятность посетить Afisha.ru явно больше, чем у пожилых людей, проживающих в небольших городах. Таким образом, если при формировании выборки набрать людей из определенной группы больше, чем эта группа представлена во всей интернет-аудитории, вероятность p окажется смещенной в сторону этой группы аудитории, и все последующие расчеты окажутся неприменимы для всей интернет-аудитории.
Резюме:
1. Панельные исследования хороши для оценки крупных сайтов. Чем меньше аудитория сайта, тем выше погрешность измерения.
2. Не нужно воспринимать абсолютные значения, полученные в результате панельного исследования, как некое среднее или точное значение. Всегда считайте доверительный интервал, в котором будет лежать реальное значение оцениваемого охвата сайта.
3. Не нужно слишком доверять панельным исследованиям, которые не публикуют данные своей панели (к таким исследованиям относятся упомянутые сервисы alexa.com, webomer.ru и netchart.ru). Если вы не знаете количество пользователей в панели и насколько панель репрезентативна, вы не можете понять, насколько точную оценку даст такое исследование, а это значит, что результаты таких исследований ничем не лучше, чем известный метод экспертной оценки «пальцем в небо».

